Engineering Challenge
This classic two dimensional driven cavity test case is documented in literature by Ghia [1]. The fluid motion in the cavity is driven by shear forces due to a moving wall boundary condition at the top of the cavity. Figure 1 details the geometry of the cavity along with the dashed lines Dh and Dv showing where data is taken for comparison.
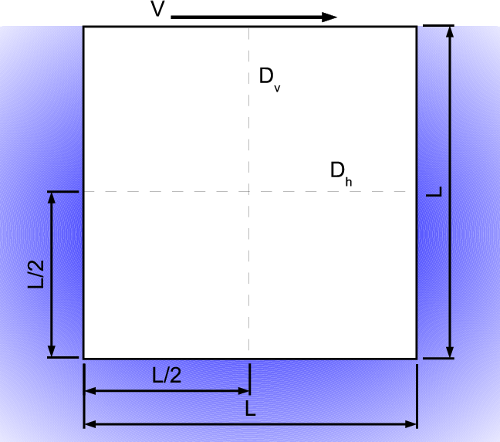
Figure 1
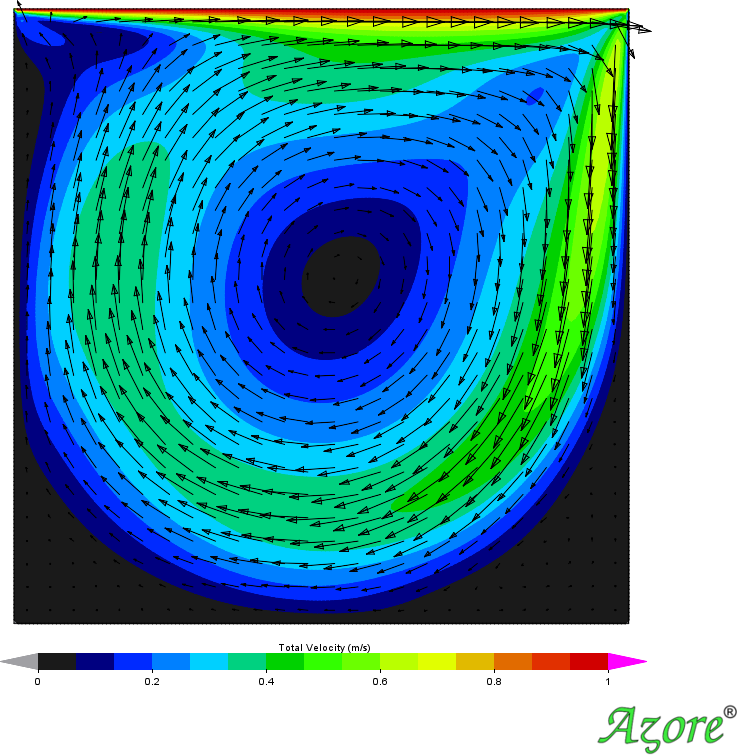
Figure 2
Azore Solution
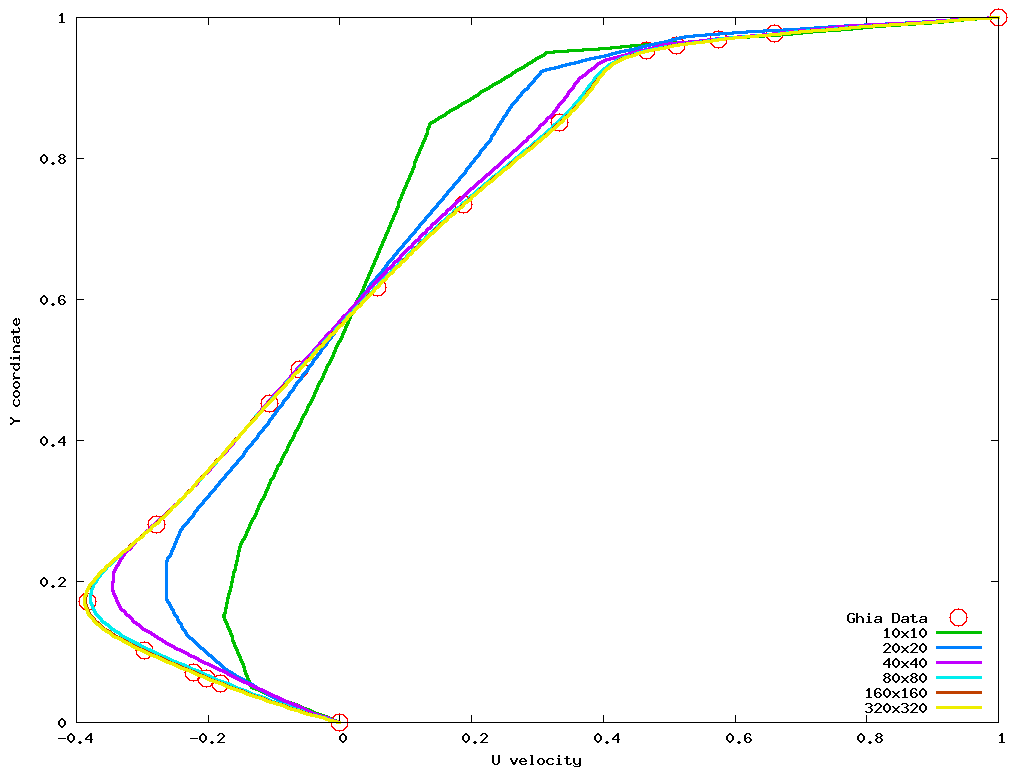
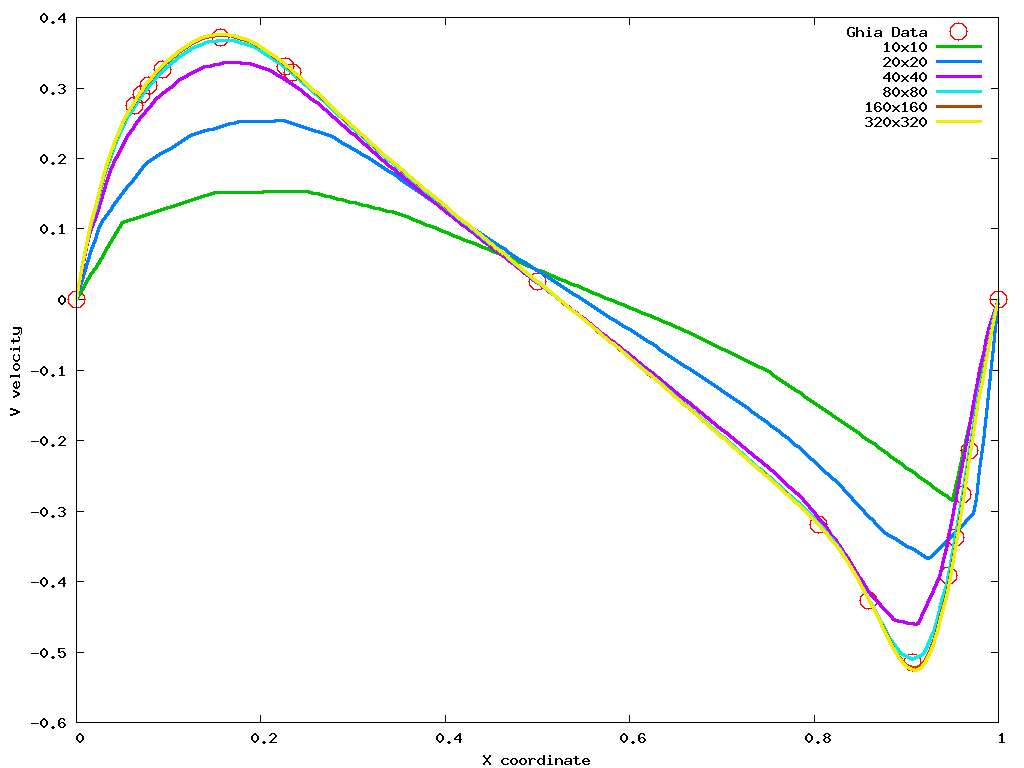
The Reynolds number of the cavity is used to classify the flow in the square cavity. A systematic grid refinement via six different uniformly spaced square control volume mesh topologies are considered (10x10, 20x20, 40x40, 80x80, 160x160, and 320x320).
The figures below show line graphs of the horizontal velocity predicted by Azore for each mesh density. These results in general show the accuracy of Azore and that a grid independent solution is achieved with the 80x80 mesh density with only small improvements in solution fidelity as the mesh density is doubled to 160x160 and 320x320.