Engineering Challenge
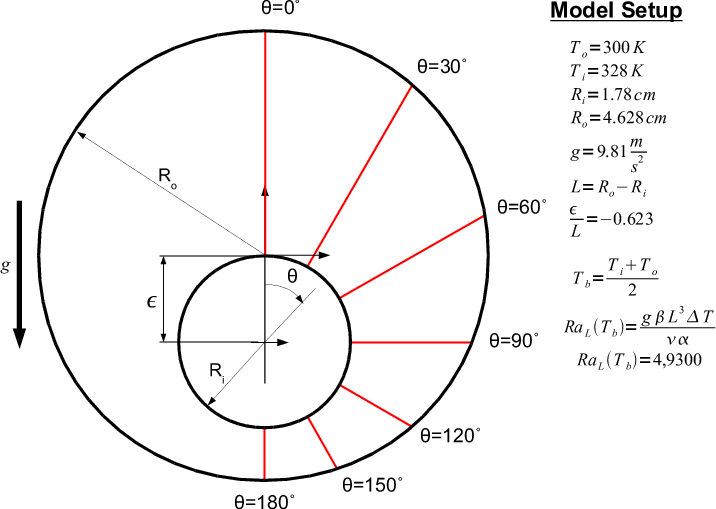
This case simulates the buoyancy driven flow of nitrogen in a horizontal cylindrical cavity. A two dimensional cross section is shown below. This geometry consists of two cylinders, a large and small, one inside the other. The smaller cylinder acts as a heat source and is placed inside the larger cylinder to promote fluid motion.
Azore Solution
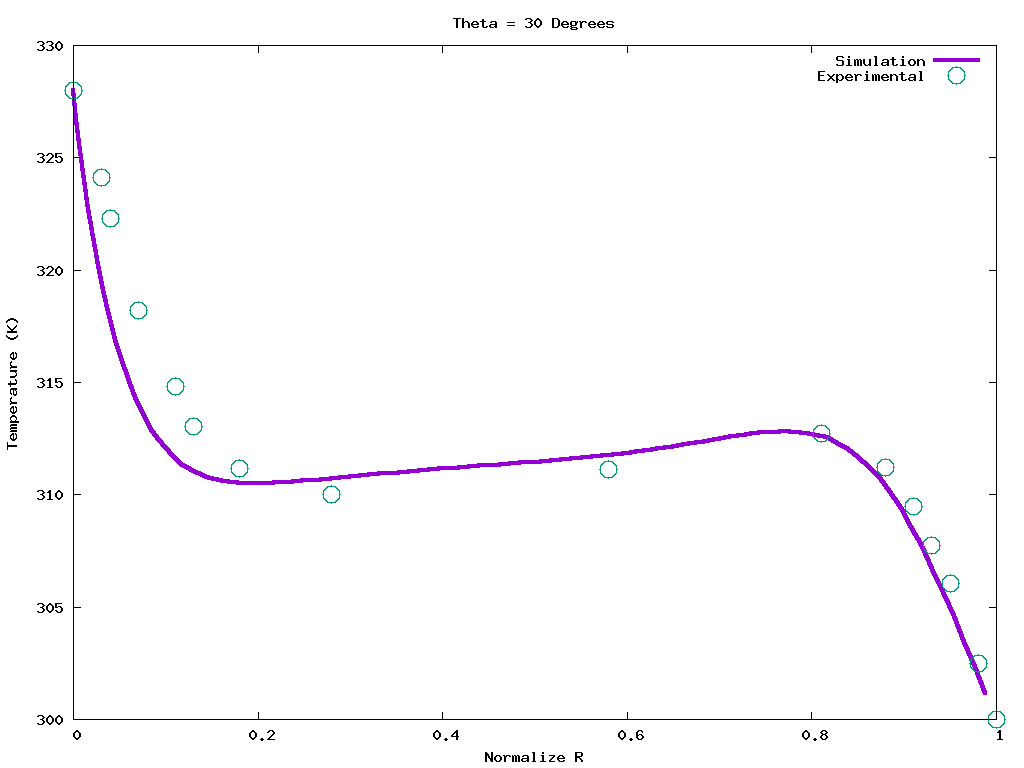
The flow is laminar with a Rayleigh number of 49,300 and a Prandtl number of 0.706. The flow field inside the cavity is assumed to be two dimensional for this modeling effort. The model domain was discretized using polygonal mesh topology consisting of 5,849 cells and 34,140 faces.
Nitrogen was assumed to be an ideal gas. The cavity pressure was assumed to be constant at atmospheric pressure. The density was assumed to vary according to the ideal gas law. The laminar viscosity was assumed to follow Sutherland's law. A 4th order polynomial for the specific heat of nitrogen was used. The incompressible SIMPLE method was used to couple the momentum and continuity equations. A second order up-winding method was used for the velocity and temperature fields. The inner cylinder was given a constant temperature Tinner=328 K and the outer cylinder was fixed at Touter=300 K. The figures below validate the Azore results through a comparison to published experimental data.