Engineering Challenge
This validation is inspired by the experimental work of J.S. Jayakumar et al. The geometry consists of a small tube that is coiled in a circular arrangement inside an insulated stainless steel shell. Two separate fluid paths are present: one in the tube and one outside the tube (in the shell). Hot water is injected at the inlet of the tube, while cool water flows into the shell.
The objective is to predict the temperature at each outlet. The key challenges for simulating this case are summarized by:
- Simulating multiple flow paths
- Solving for conjugate heat transfer through the material thickness of the tube
- Modeling turbulent flow
- Proper modeling of fluid and solid material properties
- Applying an effective meshing strategy
- Temperature dependent properties
Azore Solution
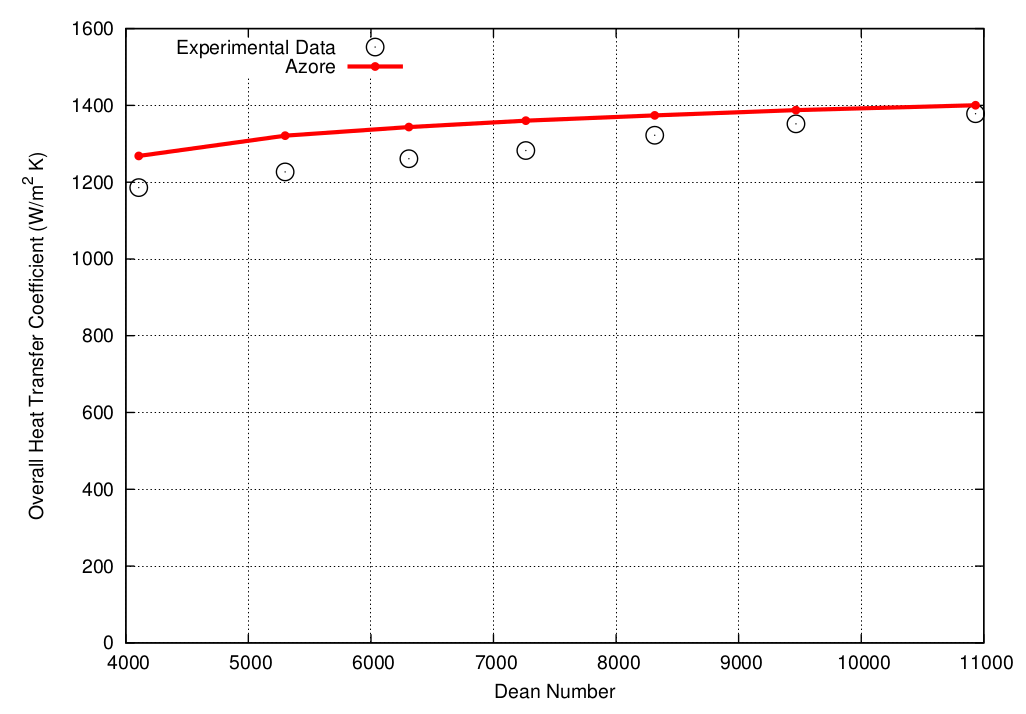
As shown below, Azore CFD accurately predicts the outlet temperatures by simulating the conjugate heat transfer between the multiple flow paths in this study.
Several Azore capabilities are key to producing an accurate and efficient solution:
- Polyhedral solver
- Piecewise temperature dependent fluid properties
- Turbulence modeling with wall function
- Thin wall modeling with effective thermal thickness